MAKALAH FUNGSI DAN MACAM-MACAM FUNGSI SERTA APLIKASI FUNGSI PERMINTAAN DAN FUNGSI PENAWARAN

  

FUNGSI :

Fungsi yaitu hubungan matematis antara suatu variable dengan variable lainnya.Unsur-unsur pembentuk fungsi, yaitu variable, koefisiensi, dan konstanta. Yang dimaksud dengan variabel adalah unsur yang sifatnya berubah-ubah dari satu keadaan ke keadaan lainnya. Koefisien adalah bilangan atau angka yang diletakkan tepat didepan suatu variable terkait dengan variabel yang bersangkutan. Konstanta sifatnya tetap dan tidak terkait dengan suatu variabel apapun.

Secara umum jika dikatakan bahwa y adalah fungsi dari x maka ditulis y = f(x),dimana x adalah suatu variable dan y adalah variabel terikat.         

a. 3y = 4x–8,               y adalah variabel terikat

x adalah variabel bebas

3 adalah koefisien ( terletak didepan variabel  x )

4 adalah koefisien ( terlatak didepan variabel  x )

-8 adalah konstanta

b.  y = X ½,                   y adalah variabel terikat

x adalah variabel bebas.        

Jika x adalah fungsi dari y maka ditulis x = f (y), dimana y adalah variabel bebas danx adalah variabel terikat.

Pendefinisian fungsi dapat dilakukan dengan beberapa cara:

(1) Didefinisikan sebagai relasi yang memenuhi sifat tertentu;

(2) Dengan rumus dan grafik Cartesius;

(3) Sebagai pasangan berurutan;

(4) Dengan diagram panah

MACAM-MACAM FUNGSI :

1.Fungsi Aljabar

Y disebut fungsi aljabar dari X jika Y adalah suatu akar dari suatu persamaaan derajat tinggi dalam tinggi yang koefisien-koefisiennya adalah suku-suku dari X.

Contoh :

*Fungsi aljabar bulat rasional :

Y = X² 5X + 7

Y = 1/3X³ + X² + 4X + 1

*fungsi aljabar ecah rasional :

Y = X – 1

      3X +1

Y = X² + X – 3

          X + 5

CONTOH SOAL FUNGSI ALJABAR :

Tentukan turunan pertama dari fungsi berikut:
a) f(x) = 5(2x² + 4x)
b) f(x) = (2x + 3)(5x + 4)

Pembahasan
Tentukan turunan pertama dari fungsi berikut:
a) f(x) = 5(2x² + 4x)
f(x) = 10x² + 20x
f ' (x) = 20x + 20

b) f(x) = (2x + 3)(5x + 4)

Urai terlebih dahulu hingga menjadi
f (x) = 10x² + 8x + 15x + 12
f (x) = 10x² + 13x + 12

Sehingga
f ' (x) = 20x + 13

2.Fungsi Linear

Yang dimaksud dengan fungsi linear atau fungsi garis lurus adalah suatu fungsi dimana variabel bebasnya paling tinggi berpangkat satu. Grafik dari fungsi linear ini apabila di gamber suatu garis lurus.

*Bentuk umum dari fungsi linear Y = f(x) adalah Y = ax + b di mana :

-          A dan b adalah konstanta

-          X adalah variabel bebas

-          Y adalah variabel tidak bebas

*ciri-ciri fungsi linear :

a)      Pada X = 0, maka Y = b meupakan titik potong antara fungsi dengan sumbu Y.

b)      Bilangan a merupakan arah dari fungsi disebut koefisien arah atau tg @

c)      Lukisan fungsi linear selalu berupa garis lurus.

CONTOH SOAL LINEAR :

*Bila diketahui Y = 5X + 5 maka grafik dari fungsi ini dapat diambarkan dengan menggunakan tabel X dan Y atau dengan ciri-ciri :

a. Titik potong dengan sumbu X, maka Y = 0

5X + 5 = 0

5X = -5

X = -1 .............. ( -1 , 0)

b. titik potong dengan sumbu Y, maka X = 0

Y = 5 ...............( 0, 5 )

c. Koefisien arah 5

3.Fungsi Kuadrat

Fungsi kuadrat adalah suatu fungsi non- linear (garis tidak lurus) yang variabel bebasnya berpangkat dua. Grafik dari fungsi kuadrat jika di gambar merupakan garis tidak lurus yang berbentuk parabola. Bentuk umum fungsi kuadrat dapat di rumuskan :

a)      Y  = f(x) adalah Y = aX² + bX + c

Di mana :                    

Y                = Variabel tidak bebas

X                = Variabel bebas

A,b,c          = Konstanta (bilangan konstan)

b)      X = f(Y) adalah X = AY² + BY + C

 CONTOH SOAL  FUNGSI KUADRAT :

Tentukan fungsi kuadrat yang memotong sumbu x di titik A(-8,0);(6,0) serta memotong sumbu Y di titik C(0,3).....???

Pembahasan :

4.Fungsi Pecah

Fungsi pecah adalah suatu fungsi non-linear (garis tidak lurus) yang variabel bebasnyamerupakan penyebut. Grafik dari fungsi pecahan ini apabila di gambar merupakan garis tidak lurus yang berbentuk hiperbola.

Bentuk umum dari fungsi pecah adalah Y = f(x)

                              Y= ax + b

                                    Cx +d

Di mana:

-          A,b,c adalah konstanta

-          X adalah variabel bebas

-          Y dalah variabel tidak bebas

CONTOH SOAL FUNGSI PECAH :

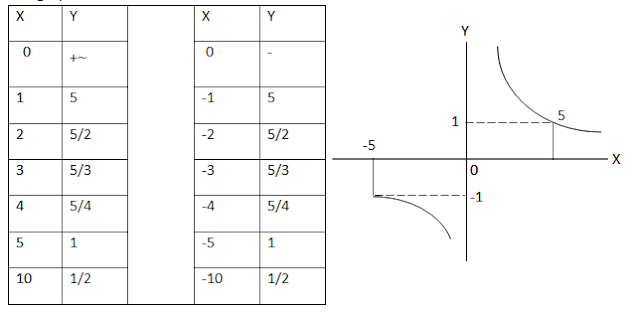
 *Tentukan grafik dari fungsi pecah apabila diketahui y = 5/x

Pembahasan :

- Titik potong dengan sumbu Y adalah pada X = 0, maka Y = -, jadi titik potongnya P ( 0,- )

- Titik potong dengan sumbu X adalah Y = 0, maka X = -, jadi titi potongnya Q ( -,0 )

- Asimtot tegak adalah bila Y = - maka X = 0, jadi persamaan garis asimtot tegak adalah X = 0 sama atau berhimpit dengan sumbu Y

- Asimtot datar bila X = -, maka Y = 0, jadi persamaan garis asimtot datar adalah y = 0 sama atau terhimpit dengan sumbu X

Dengan bantuan ciri-ciri ini dan dengan bantuan tabel X dan Y kita dapat melukis grafik fungsi pecah.

5.Fungsi Eksponensial

Fungsi eksponensial merupakan suatu bentuk fungsi dari f(x)=a^x ,di mana a adalah suatu konstanta positif yang di kenal  sebagai fungsi  pokok.Jadi suatu fungsi  eksponensial pada dasarnya berbeda dengan fungsi pangkat f(x)=x”, di mana pokoknya adalah variabel dan pangkatnya adalah konstanta.

*CONTOH SOAL EKSPONENSIAL :

3⁴         = 3.3.3.3 = 81

4^1/2       = = 2

4^-3/2      ==

4^3/2       = ()³ = 2³ = 8

6.Fungsi logaritma

Fungsi ini berperan pada persoalan-persoalan statistik dan probabilitas. Dan lebih banyak kepada persoalan-persoalan diskrit. Contoh: bagaimana mengatur agar antrian pembelian bensin sedemikian sehingga pada saat-saat tertentu pegawai pelayanan diperbanyak. Misal pada pembayaran rekening listrik, para konsumen lebih banyak membayar pada akhir tagihan daripada awal-awal penagihan. Sangat bijak manajer mengatur agar pada hari-hari terakhir pegawainya hrus membantuk bagian kasir untuk melayani konsumen.
Perhatikan dua deret berikut :

*Deret hitung : 0 1 2 3 4 5 6 . . . . . . . . .

*Deret ukur : 1 3 9 27 81 243 729 . . . . . . .

Apabila bilangan deret hitung dianggap sebagai pangkat (eksponen/ power ) dari 3, maka akan di peroleh bilangan deret ukur dengan jelas memberikan pangkat kepada angka 3 tersebut, hasilnya sebagai berikut :

CONTOH SOAL LOGARITMA :

*Jika log 2 = 0.301 dan log 3 = 0.477, maka     log 3 225 = 

 Pembahasan :

 log  =  log 15   =  log 15 

                       =  log 5.3 

          =  (log 5 + log 3) 

           =   (log  + log 3) 

            = ( log 10 – log 2 + log 3)

            =  ( 1 – 0.301 + 0.477) 

            =  (1.176) = 0.784

1.Fungsi permintaan ( Demand )

Fungsi permintaan menunjukan adanya hubungan antara variabel biaya (price) dengan jumlah kondisi barang ,jasa (quantity) yang di minta dan berlaku terhadap seorang konsumen (pemakai barang).

hubungan antara harga barang  (p) dengan jumlah barang yang diminta (Q) sebagai  x = Q(p). X = sumbu horizontal sebagai jumlah barang dan y = sumbu vertikal harga barang. Hal tersebut di atas di kemukakan oleh Antonie Agustin Cournot (1801-1877). Bentuk umum permintaan adalah :

                                                                                                P = a - bx

dengan            P   = Price (harga)                                          P = a - bQ

                         x    = Quantity (jumlah barang)

                        a,b = Konstanta

Dari bentuk umum fungsi permintaan P (price) harga sangat tergantung dari jumlah barang (Q = quantity) yang diminta di pasaran.

Hal tersebut berkenaan dengan hukum permintaan, yakni : “Bila harga barang naik maka jumlah permintaan akan turun, dan sebaliknya bila harga barang turun maka jumlah permintaan akan bertambah”.        

                                                                                                                             

Perhatikan gambar grafik fungsi permintaan                                                    

a.      Bentuk umum fungsi permintaan linear P = a – bQ

b.      Kuadran yang berlaku hanya kuadran I (dalam dunia

Ekonomi tidak berlaku harga barang dan jumlah bernilai

Negatif)

c.       Gambarnya tidak condong ke kanan (gradiennya negatif)

d.      Harga (P) maksimal apabila jumlah barang minimal :

P _maks apabila Q = 0

e.      Jumlah barang (Q) maksimal apabila harga barang minimal

Q _maks apabila P = 0

*contoh soal :

Diketahui P = -8Q + 600 adalah fungsi permintaan, maka :

a. gambarkan fungsi tersebut !

b. tentukan harga barang bila jumlah yang diminta sebanyak 50 !

c. tentukan harga maksimal !

d. tentukan jumlah maksimal barang bila barang bebas di pasaran !

jawab :

a.P = -8Q + 600

Titik potong ada sumbu Q           P = 0

Q = -8Q + 600

8Q =

Q = 75

Memotong sumbu Q di titik (75,0)

Titik potong ada sumbu P             Q = 0

P = -8Q + 600

P = 600

Memotong pada sumbu P di titik  (Q,600)

Gambar grafiknya di samping :

b. Harga barang = P, jumlah di minta Q = 50

Q = 50             P = -8Q + 600                                                                                                                          

                          P =-8 . 50 + 600                                                                            

                          P = -400 + 600

                          P = 200

Jadi, apabila jumlah yang di minta = 50 satuan barang, maka harganya = 200 satuan harga

c.harga maksimal, jika jumlah yang diminta minimal = 0

Q = 0               P = -8Q + 600

P = -8 . 0 + 600 = 600

Jadi, harga maksimal adalah 600 satuan harga

d.Barang bebas di pasaran, harga minimal = 0

P = 0                P = -8Q + 600

                                0 = -8Q + 600

                                8Q = 600

                                X =

                                X = 75

Jadi, barang bebas di pasaran jika jumlah barang 75 satuan barang.

 2. Fungsi penawaran (Supply )

Untuk fungsi penawaran barang  (supply) merupakan hubungan antara harga suatu barang  (price ) dengan jumlah komoditas (barang dan jasa) atau Q yang di tawarkan.Dalam fungsi penawaran yang berlaku pada seorang produsen ( penghasil barang) akan berkaitan dengan hukum penawaran ,yakni “ bila harga naik, maka penawaran akan bertambah,dan sebaliknya bila harga turun ,maka penawaran akan berkurang.

                                                                P = A + bQ           atau       P = a + bx

P             = (price) harga per unit

x/Q        = jumlah barang

a,b          = Konstanta

akan diperoleh grafik sebagai berikut ;

Dari grafik di atas, maka :

1. Bentuk umum fungsi penawaran linear P = a + bx, P = a + bX
2. Berlaku hanya di kuadran 1 (baik harga maupun yang ditawarkan tidak mungkin negatif)
3. Untuk gambar grafiknya condong ke kanan (besar gradiennya positif)
4. Untuk harga minimal akan diperoleh apabila jumlah barang juga minimal. P minimal bila x/Q minimal (harga maksimal tidak ada)

Contoh soal penawaran ???

1.Diketahui fungsi suatu barang dirumuskan Q = P² – 64

a.Gambarkan grafiknya !

b.Tentukan penawaran pada posisi harga 12 !

c.Tentukan harga barang bila penawaran 36 !

d.Tentukan harga bila tidak ada penawan !

jawab :

a.Q = P2 – 64

Titik potong pada sumbu P      Q = 0

P² – 64 = 0

P² = 64

P =

P₁ = -8, P₂ = 8                                                                                                  

Memotong pada sumbu P di titik (0,-8), dan (0,8)

Titik potong ada sumbu Q →  P = 0

Q = P2 – 64

Q = 02 – 64

Q = -64

Memotong pada sumbu Q di titik (-64,0)

Gambar grafiknya :

b.Penawaran pada  posisi 12

Q=P2-64, P=12                  Q=p²-64

                                                   =12²-64

                                                   =144-64

                                                Q =80

Jadi,apabila harga 12 suatu barang maka penawaranya adalah 80 satuan harga.

 c. harga barang, bila penawaran = 36

Q=P²-64, P=36 à 36=P²-64

                                36+64=P²

                                100    =P²

                                P= 

                P₁=10,P₂=-10

Apabila tidak ada penawaran maka harganya adalah 10 satuan.

d.Tidak ada penawaran Q=0

                                Q= P²-64

                                0= P²-64

                                P²=64

                                P=,P = 8

Jadi harganya 8 satuan.

DAFTAR PUSTAKA :

1.SURANTO EDY,2006. MATEMATIKA BISNIS & MANAGEMEN,YUDISTIRA

2.DESMIZAR,S.E,.M.M,MARET 2003, MATEMATIKA UNTUK EKONOMI DAN BISNIS,JAKARTA,RINEKA CIPTA

Share this post